本章知识点 :> 逻辑思维
这节课会比较轻松
第3章和第4章讲 逻辑思维 ,其实还是对 简单重复 的练习,上一章我们过了5个思维训练,这一章再过5个。
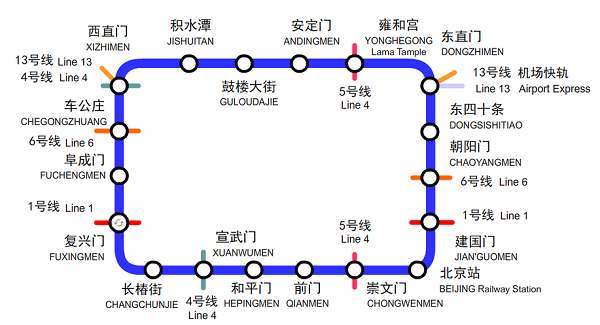
(没错,我们这节课来做2号线)
高斯小王子

我们从一个 "数学王子",高斯的故事开始说吧。
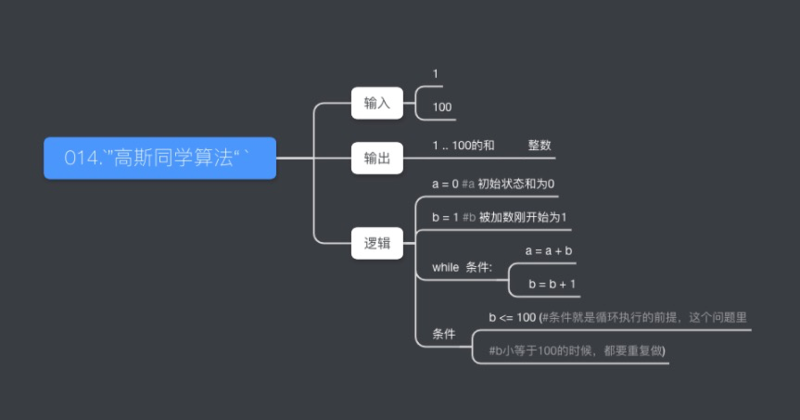
有一次数学课堂上,老师要求计算 1 + 2 + 3 + .... 100 ;也就是从1加到100,求和。
高斯很聪明,这么算的 (1+100)*50 (算式)
而高斯的同学呢,则是这么算的,1+2 = 3, 3+3 = 6, 6 + 4 = 10, ..... (循环)
请你把这两种方法用Python程序来表示
- 思考一下这么写:
sum = 1 + 2 + 3 + .... 100能计算出结果吗?(答案是不能) - 初学者确实很容易犯类似的错误,我们可以看着这个算式的问题在哪?
....这个表示法,我们在Python里是找不到对应的运算的。(这是典型的人可以读懂,但Python读不懂)高斯的算法
sum = (1+100)*50
print(sum)
- 高斯同学的算法
- 我们第一感觉是要用循环来做,但是第二感觉是没法一下写出来
循环程序的关键是把要重复执行的逻辑抽象出来,在这个例子里,重复的事1+23+36+4..- 我们可以抽象出来每次重复的事其实是
a + b;其中a是到前一步为止算得的和 b是234...100换言之,就是每次循环b就加1
- 尝试写出代码:
- 易错点:很多人可能会在条件是
b < 100还是b <= 100犯迷糊,其实完全可以写一个,最后把b打印出来看一下 - 如果不对,再改改(这就是基本的程序调试过程)
试一下 在线Python
a = 0 #和为0b = 1while b <= 100:a = a + b #求和b = b + 1 #加1 print(a)
晨跑习惯

很多人有早晨跑步的习惯,下面的一段话记录了小明今天晨跑的情况,请你用Python来计算一下
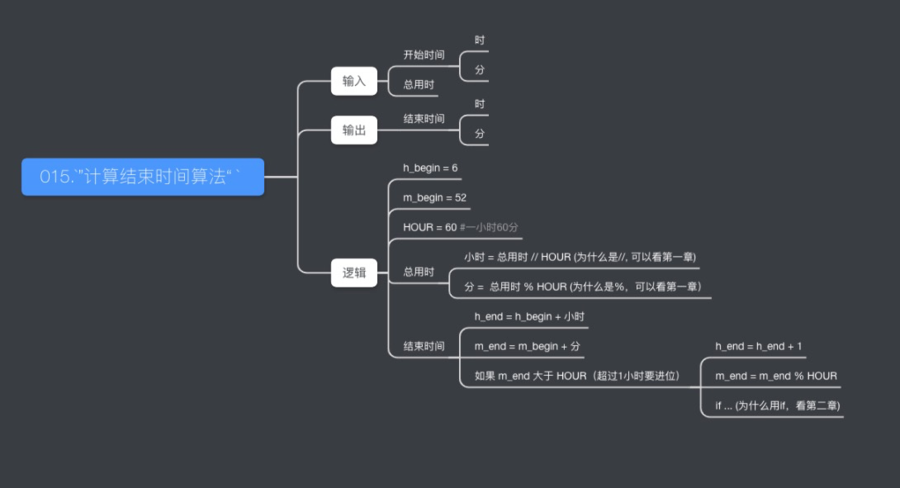
我早上六点五十二分出家门,以8:15的节奏跑了一英里,又以7:12的节奏跑了三英里,然后又是8:15的节奏跑了一英里,回到家吃饭是几点?
8:15 的节奏表示 8/15 小时每英里,其实就是速度。 跟我
代码块思想,我们把这个问题分为 计算结束时间算法 和 计算总用时算法计算结束时间算法 输入:开始时间(注意是小时和分),总用时(分)
- 变成代码
h_begin = 6
m_begin = 52
HOUR = 60
total = 8/15 * 60 * 1 + 7/12 * 60 * 3 + 8/15 * 60 *1
total = int(total) #一定要先转int整型
h = total // HOUR
m = total % HOUR
h_end = h_begin + h
m_end = m_begin + m
if m_end >= HOUR: #注意是>=
h_end = h_end+1
m_end = m_end % HOUR
print(str(h_end) + "点" + str(m_end) + "分" #还记得str吗?
试一下 在线Python
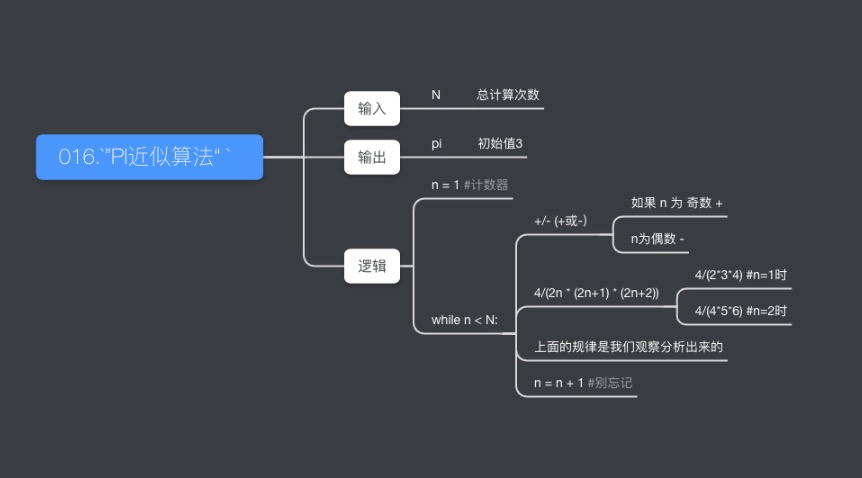
PI的计算
`
我们用一个圆周率算法来计算出pi的近似值
我们定义变量pi
算法规律如下 π = 3 加 4除以(2*3*4) 减 4除以(4*5*6) 加 4除以(6*7*8) 如此往复
现在要求你写出算式,计算出结果
- 熟悉
循环设计的朋友可以尝试识别一下这个算法里重复的运算是什么? -
+ 4/(2*3*4) -
- 4/(4*5*6) -
+ 4/(6*7*8) - 我们需要一个循环的计数
n刚开始n = 1 -
+ 4/(2*3*4) #n=1时 -
- 4/(4*5*6) #n=2时 -
+ 4/(6*7*8)#n=3时` - 找一找n和算式的关系(或者说规律), 我们就可以抽象的表示每次重复的事情了!
- 注意:
n%2 == 1表示奇数(想一下为什么?)
pi = 3
N = 100
n = 1
while n < N:
if n%2 == 1:
pi = pi + 4/(2*n * (2*n+1) * (2*n+2))
if n%2 == 0:
pi = pi - 4/(2*n * (2*n+1) * (2*n+2))
n = n + 1
print(pi)
试一下 在线Python
- 易错点:计算2n+1 不要写成
2n+1,一定要写2*n +1(这是典型的人类思维和程序思维之间的差别)
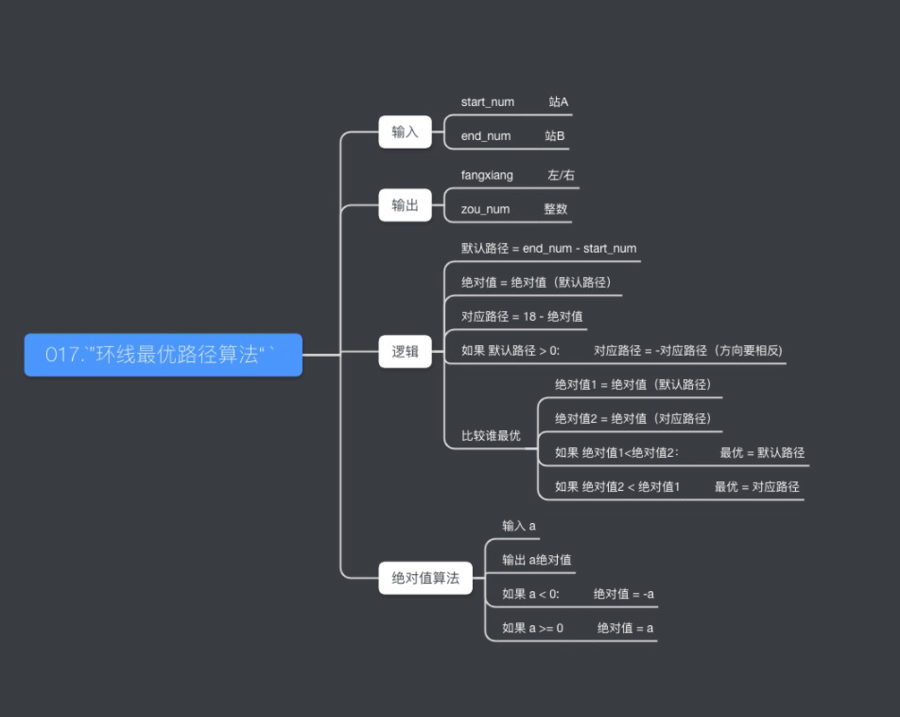
地铁2号线

”前门“ 1号,”崇文门“ 2号 ...
地铁2号线的问题显然比1号线要复杂一点,因为它是环线从
A站 到 B站两个方向都可以达到,我们的程序需要选出最优的路线给乘客
- 思路:先取名
环线最优路径算法 - 输入:
startend输出fangxiangzou_num
start = '?' #具体执行时填写
start_num = ? #具体执行时填写
end = '?' #具体执行时填写
end_num = ? #具体执行时填写
fangxiang = ''
zou_num = 0
if start_num == end_num:
print("现在出站")
#环线最优路径算法
a = 0
while a < zou_num:
print(fangxiang+'走1站') #一定要4个空格
a = a + 1
- 现在我们来攻克
环线最优路径算法 - 思路:一共18站,假设起始站
A,终点B - 我们先尝试去计算
B - A;对照图看一下,比如 A=1 B=5;B-A 为 4 - 或者 A=17 B=1 ;B - A 为 -16
- 我们注意到 B-A 大于0,表示右行,小于0表示左行。(可以看做默认路径)
- 当然因为,这个是环线,所以任何一个默认走法,都都应一个反方向的走法
4 -> -14 ; -16 -> 2 (默认走法和反方向的走法肯定是一正一负,但绝对值的和为18)
总结:假设起始站
A,终点B- 默认路径:
B-A;对应路径(需要计算) - 比较
默认路径和对应路径看谁最优 (需要计算) - 如果 路径 > 0 右行
- 如果 路径 < 0 左行
- 另外:需要一个
绝对值算法(1是用在对应路径计算,1是用在最后的走几站的计算)
- 代码实现
start = '?' #具体执行时填写
start_num = ? #具体执行时填写
end = '?' #具体执行时填写
end_num = ? #具体执行时填写
fangxiang = ''
zou_num = 0
if start_num == end_num:
print("现在出站")
#环线最优路径算法
default = end_num - start_num #默认
jueduizhi = default #默认绝对值
if default < 0:
jueduizhi = -default #默认绝对值
duiying = 18 - jueduizhi #对应的绝对值
if default > 0:
duiying = -duiying #反方向
j1 = default
if defalut <0:
j1 = -default #绝对值1
j2 = duiying
if duiying <0:
j2 = -duiying #绝对值2
zuiyou = 0
if j1 < j2:
zuiyou = default
if j2 < j1:
zuiyou = duiying
if zuiyou > 0:
fangxiang = '右'
zou_num = zuiyou
if zuiyou < 0:
angxiang = '左'
zou_num = -zuiyou
a = 0
while a < zou_num:
print(fangxiang+'走1站') #一定要4个空格
a = a + 1
试一下 在线Python